El movimiento juega un papel importante en muchas de las actividades que realizamos a diario. Continuamente, estamos ante situaciones de objetos que se mueven: se trasladan, giran o se reflejan.

 

Los movimientos básicos de la geometría plana son: Traslaciones, Giros o Rotaciones y Simetrías o Reflexiones. A los tres movimientos anteriores se une el movimiento compuesto denominado Simetría con deslizamiento y el movimiento conocido con el nombre de Simetría central, que realmente es un giro. A continuación, aparecen descritos los cinco movimientos anteriores.

 

 La traslación (Traslation en inglés):

 

Podemos pensar en la traslación como en un deslizamiento. A diario, tenemos muchas experiencias de desplazamientos: cuando abrimos un cajón, cuando bajamos o subimos una persiana, en los deportes de patinaje...

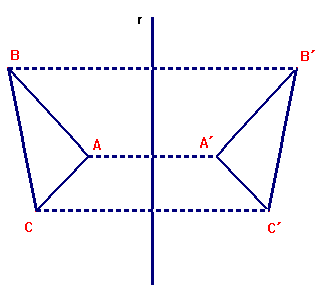
Para estudiar este movimiento con algo más de detalle, vamos a restringirlo al plano. Consideraremos el deslizamiento de un cuadrilátero que se desplaza desde el punto A al  A`.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

La traslación se realiza en una determinada dirección y sentido y el cuadrilátero recorre una

determinada distancia. En este caso:

* La dirección es la que marca la recta que pasa por A y por A`.

* El sentido es el que va de A a A` , es decir hacia la derecha.

* La distancia recorrida es la que separa los puntos A y A`.

Para trasladar una figura necesitamos dar, por tanto, una flecha o vector , ya que dicha flecha marca todos los elementos necesarios para realizar la traslación:

* Una dirección: la de la recta que contiene al vector.

 

* Un sentido: el que marca la punta de la flecha (hacia la derecha).

 

* Una distancia: la determinada por la longitud de la flecha.

 

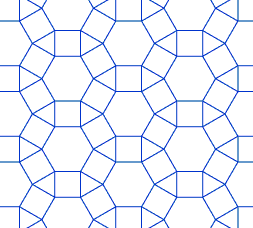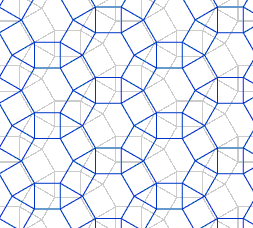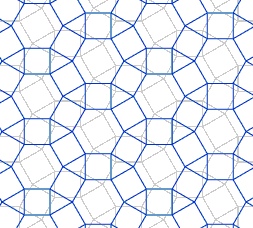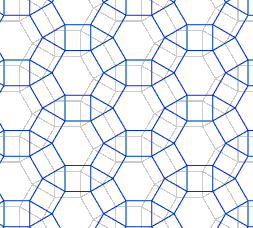
En la animación siguiente se puede observar como el mosaico de la figura queda invariante o se superpone mediante traslación:

 

 

 

 

 

 

 

 La rotación o giro:

 

Tenemos ejemplos de giros en muchas de nuestras actividades cotidianas. Al conducir un coche: el volante, la manivela de la ventanilla o las propias ruedas realizan movimientos de giro; al abrir una puerta,...

En el plano, un giro viene determinado por el centro de giro (un punto) y por el ángulo de giro.

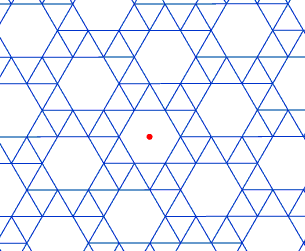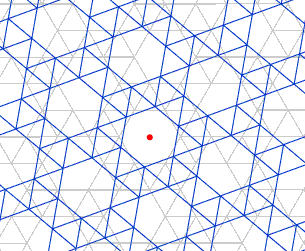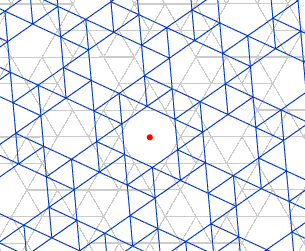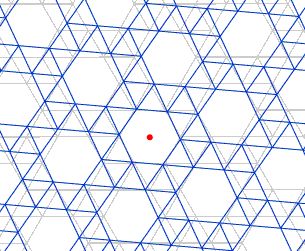
Podemos realizar un movimiento de rotación, con centro un punto O y amplitud 60º, sobre el triángulo ABC, en la forma que se indica en la figura siguiente:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

En la animación, se puede observar como el mosaico de la figura queda invariante mediante rotación

 

 

 

 

 

 

 

 

 

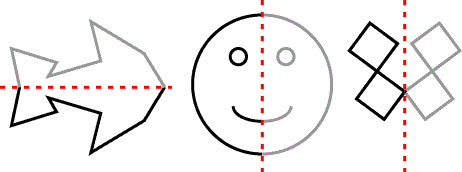
 La reflexión o simetría axial (Reflection en inglés)

En la vida también tenemos bastantes ejemplos de simetría o reflexión, sobre todo en la imagen de los espejos.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Podemos realizar una reflexión de eje la recta  r  sobre un triángulo ABC, en la forma que se indica en la figura: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

En el gráfico se muestra un mosaico que queda invariante mediante la simetría axial que tiene por eje la línea marcada en rojo: